Valoreseptorin toimintakäyrä

Pimeävirran muutos valosalaman seurauksena on luonteeltaan kuvan 2.3(b) mukainen signaali. Vaste nousee maksimiinsa nopeasti valosalaman jälkeen ja palaa hitaammin takaisin nollatasolle. Usein vasteista halutaan tietää vain amplitudiparametri: pimeävirran maksimipoikkeama nollatasosta. Maksimipoikkeama U stimuloivan valosalaman intensiteetin I funktiona noudattaa varsin hyvin Michaelis-yhtälöä:

$$U(I) = U_{max}\frac{I}{I+I_s}$$

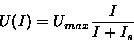
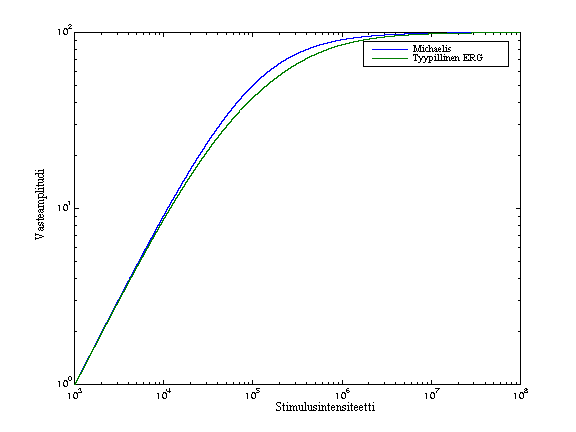
missä U_max on vasteen saturoitunut maksimi (suurin mahdollinen vaste) ja I_s on se intensiteetti, jolla saadaan maksimin puolikkaan suuruinen vaste eli U(I_s) = U_max/2. Yhtälön määrittämää kuvaajaa kutsutaan yleisesti solun toimintakäyräksi. Toimintakäyrä esitetään yleensä loglog-asteikolla kuvan 2.7 mukaisesti. Kuten kuvasta nähdään heikoilla stimuluksilla vasteen amplitudi riippuu likimain lineaarisesti intensiteetistä. Voimakkailla stimuluksilla vaste saturoituu, jolloin stimuluksen kasvattaminen ei enää kasvata vastetta.

  

Kuva 2.7: Michaelis-yhtälön mukainen stimulus/vaste -käyrä sekä tyypillinen eristetystä verkkokalvosta saatava käyrä ovat hyvin lähellä toisiaan. Amplitudiakselin arvot ovat prosentteja maksimista. Intensiteettiakselin yksikkö on valittu mielivaltaisesti.

Mittaamalla näköreseptorin vaste kahdella eri intensiteetillä, voidaan yhtälön parametrit U_max ja I_s määrittää ja siten määrätä myös solun toimintakäyrä. Toimintakäyrää käytetään yleisesti solun fysiologisen tilan mittarina. Erityisesti I_s muuttuu solun adaptaatiotilan mukaan, joten sitä voidaan käyttää parametrina, joka kertoo solun herkkyyden. Herkkyys määritellään yleensä toimintakäyrän lineaarisella alueella stimuluksen voimakkuuden ja stimuluksen seurauksena saadun vasteen suuruuden suhteena. Sauvasolun herkkyys voidaan siis määritellä seuraavasti:

$$S = \frac{\Delta U}{\Delta I}$$

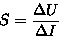
Kun intensiteetin annetaan lähestyä nollaa, saadaan Michaelis-yhtälön mukaan:

$$(U/I)_{I \to 0} = (\frac{U_{max}}{I+I_s})_{I \to 0} = \frac{U_{max}}{I_s}$$

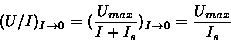
Herkkyys saa siis muodon:

$$S_0 = \frac{U_{max}}{I_s}$$

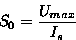
Todelliset valovasteet - erityisesti kokonaisesta verkkokalvosta mitatut - voivat poiketa hieman Michaelis-yhtälöstä. Syynä tähän ERG-mittauksilla on pääasiassa glia-solujen tuottama kontribuutio valovastesignaaliin. Syynä voi olla myös esimerkiksi preparaatin nopea adaptaatio, jolloin preparaatti valoadaptoituu jo stimulusvalon seurauksena. Tällöin preparaatin vaste voimakkaalle, muttei saturoivalle stimulukselle on pienempi kuin Michaelis-yhtälön ennustama vaste. Mittauksissa kokonaisella verkkokalvolla eri reseptorit saattavat myös saada hieman erilaisen stimuluksen tai reseptoreiden adaptaatiotila voi vaihdella. Tällöin heikoilla stimuluksilla kaikki reseptorit ovat toimintakäyriensä lineaarisella alueella tai ainakin lähellä sitä. Toisaalta voimakkailla stimuluksilla kaikki reseptorit ovat lähes saturaatiossa. Näin ollen summautuvat vasteet heikoilla ja voimakkailla stimuluksilla voivat olla malliin hyvin sopivia keskiarvoja, mutta toimintakäyrän keskiosa voi vääristyä.

Yleensä mitatut toimintakäyrät ovat loivempia kuin Michaelis-yhtälö ennustaa. Kokeellisten tulosten poikkeamista ideaalisesta pyritään yleisesti kompensoimaan ad hoc -malleilla, jotka ovat Michaelis-yhtälön yleistyksiä. Usein käytetty yleistys on potenssikorjaus:

$$U(I) = U_{max} \frac{I^n}{I^n+I_s^n}~(n < 1)$$

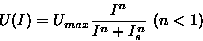
Kaavassa n on parametri, joka säätää toimintakäyrän jyrkkyyttä. Parametrin n arvolla yksi kaava yhtyy Michaelis-yhtälöön. Kaava sopii yleensä hyvin kokeellisiin tuloksiin, mutta kaavalla ei ole minkäänlaista teoreettista pohjaa. Toinen huomattavasti oleellisempi vika kaavassa on se, että vasteilla ei ole lineaarista aluetta pienillä stimuluksilla. Intensiteetin lähestyessä nollaa, vasteen ja stimulusintensiteetin suhde lähestyy ääretöntä:

$$(U/I)_{I \to 0} = U_{max}(\frac{1}{1+\frac{I_s^n}{I^{n-1}}})_{I \to 0} = \infty~(n < 1)$$

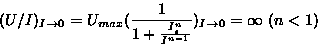
Potenssikorjaus romuttaa siis varsin oleellisen herkkyysparametrin. Yllättävän vähän käytetty z-funktio sopii hyvin kokeellisiin tuloksiin ja antaa pienille stimuluksille linearisen vasteen: [5]

$$U(I) = U_{max} \frac{I}{I+I_s\frac{1+(2-z)I/I_s}{1+zI/I_s}}$$

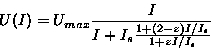
Tässä kaavassa z on säädettävä parametri ja parametrin arvolla yksi kaava yhtyy Michaelis-yhtälöön. Kun intensiteetti lähestyy nollaa saadaan stimuluksen ja vasteen suhteeksi:

$$(U/I)_{I \to 0} = (\frac{U_{max}} {I+I_s\frac{1+(2-z)I/I_s}{1+zI/I_s}})_{I \to 0} = \frac{U_{max}}{I_s}$$

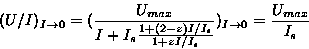
Herkkyys pienille stimuluksille on siis samaa muotoa kuin Michaelis-yhtälön tapauksessa. Tosin parametri I_s on z-funktiossa hieman pienempi kuin puolimaksimin antava intensiteetti, jos z on pienempi kuin yksi:

$$U(I_s) = U_{max}\frac{I_s}{I_s+I_s\frac{1+(2-z)}{1+z}} = U_{max}\frac{1+z}{4}$$

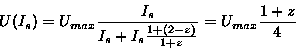
Molemmissa malleissa on yksi säädettävä korjausparametri. Jos mitattuja vasteita halutaan sovittaa esitettyihin malleihin, tarvitaan vastemittauksia siis ainakin kolmella stimulusintensiteetillä.

Jos pimeäadaptoitunutta valoreseptoria valaistaan taustavalolla, I_s kasvaa voimakkaasti, eli solu menettää herkkyyttään. Sama ilmiö tapahtuu transientisti myös stimulussalamien seurauksena. Tästä ja muista syistä johtuen mittausten kohteena olevan preparaatin toimintakäyrä muuttuu yleensä koko mittauksen ajan. Koska preparaatista voidaan kullakin ajanhetkellä mitata vaste vain yhdelle intensiteetille ja toimintakäyrän määrittämiseksi tarvitaan vaste kahdelle tai useammalle eri intensiteetille, hetkellisen toimintakäyrän suora mittaaminen on mahdotonta. Toimintakäyrän hetkelliset parametrit voidaan kuitenkin estimoida mittaamalla preparaatin vaste kahdelle tai useammalle intensiteetille mahdollisimman säännönmukaisessa sekvenssissä. Yleensä stimulussekvenssi on seuraavanlainen:

1.

Valosalama pienellä intensiteetillä.

2.

Tauko, jonka aikana pimeävirta palaa normaalitasolle.  

3.

Valosalama noin puolimaksimin antavalla intensiteetillä.

4.

Tauko, joka on yleensä hieman pidempi kuin kohdassa 2.  

5.

Valosalama intensiteetillä, joka antaa lähes maksimivasteen.

6.

Tauko, joka on yleensä huomattavasti pidempi kuin kohdissa 2 ja 4.

Stimuluksen jälkeisen tauon tulee olla yleensä sitä pidempi, mitä suurempi valosalaman intensiteetti, koska pimeävirran paluu normaalitasolle tapahtuu sitä hitaammin mitä suurempi stimuluksen intensiteetti. Kun vasteita on mitattu esitetyn sekvenssin mukaisesti, voidaan toimintakäyrä määrittää esimerkiksi pienstimulusten ajanhetkillä interpoloimalla muiden intensiteettien antamat vasteet edeltävien ja seuraavien vasteiden perusteella kyseiselle ajanhetkelle.